Background
When we began our work together in 2009, we were aware of other arts-science explorations of the genome such as Ecce Homology, a collaborative group of artists and scientists working at the intersection of comparative genomics and immersive experience, and the research done by choreographer Liz Lerman in collaboration with researchers at the NIH, Johns Hopkins University, Stanford University, Howard University, the Genetics and Public Policy Center, the Institute for Genomic Research, and the U.S. Department of Energy. The scope and achievements of these projects inspired us; however, we found our tools (drawing, dance, genomic architecture, sculpture) and our specific area of inquiry (the structure of the genome as it folds and unfolds) to be entirely separate from theirs.
Gupi: From 2009-2011, as the second artist-in-residence at the Broad Institute of MIT and Harvard, I worked closely with Erez Lieberman Aiden, collaborating with him and his team on the genome folding project. Erez had just published a paper (Lieberman-Aiden & Van Berkum et al., 2009) in which he and colleagues developed a new method for deciphering the 3-D architecture of the human genome. In that setting, Erez and his collaborators proposed a model for how the genome folds that is based on so-called space-filling curves, such as the Hilbert (Fig. 1) and Peano curves (Fig. 2).
Could I as an artist advance such a research project? When Erez used the century-old mathematical theory of space-filling curves as a way to explain how the two-meter-long human genome folds itself inside a tiny space without tangling (Clegg, 2012), I did not know how I would be able to contribute.


Erez: The objects that scientists study exist independently in the physical world, but the content of scientific theories is abstract. In order to reason about these theories and explore their implications, scientists must develop ways of representing theory. Thus, the problem of representation in science is not merely a problem of illustration, but an essential component of scientific reasoning.
Our laboratory's work on the three-dimensional structure of the human genome illustrates the challenges inherent in representing scientific concepts. Stretched end-to-end, the DNA molecules in a human cell would span two meters, but they are compressed into a space only a few microns wide. How can the human mind possibly conceive of such an extraordinary folding process?
Today, many disciplines are working together to answer this question. Mathematicians use idealized curves; physicists attempt to construct computer models; microscopists try to illuminate stretches of the genome. Gupi, too, used her particular toolset—the toolset of an artist—to work towards an answer. By directly engaging the senses, her media and her way-of-thinking opened up new avenues for understanding. Because her work is abstract—the intent is not to recapitulate a visible object—its intrinsic goal is to reveal things the eyes cannot ordinarily see.
Exploration
Gupi: While Erez spoke about the problem of genome folding in scientific and mathematical terms, I saw the genome in visual, artistic terms—as a line with area and volume that takes on a form and a shape of its own. We spent time playing with electrical wire, trying to fold it into iterations of the Hilbert and Peano curves (Fig. 3). I used rectilinear and curvilinear interpretations based on the Hilbert and Peano curves to make drawings and prints (Fig. 4). While Erez concentrated on folding the wire, and referred to it as a puzzle, I was interested in unfolding the wire as it could take countless forms. I set out to explore the concept of "unfolding": as life unfolds, as the genome continuously moves and unfolds to interact and give instruction to the machinery of the cell, and as scientific discovery unfolds at the Broad Institute.

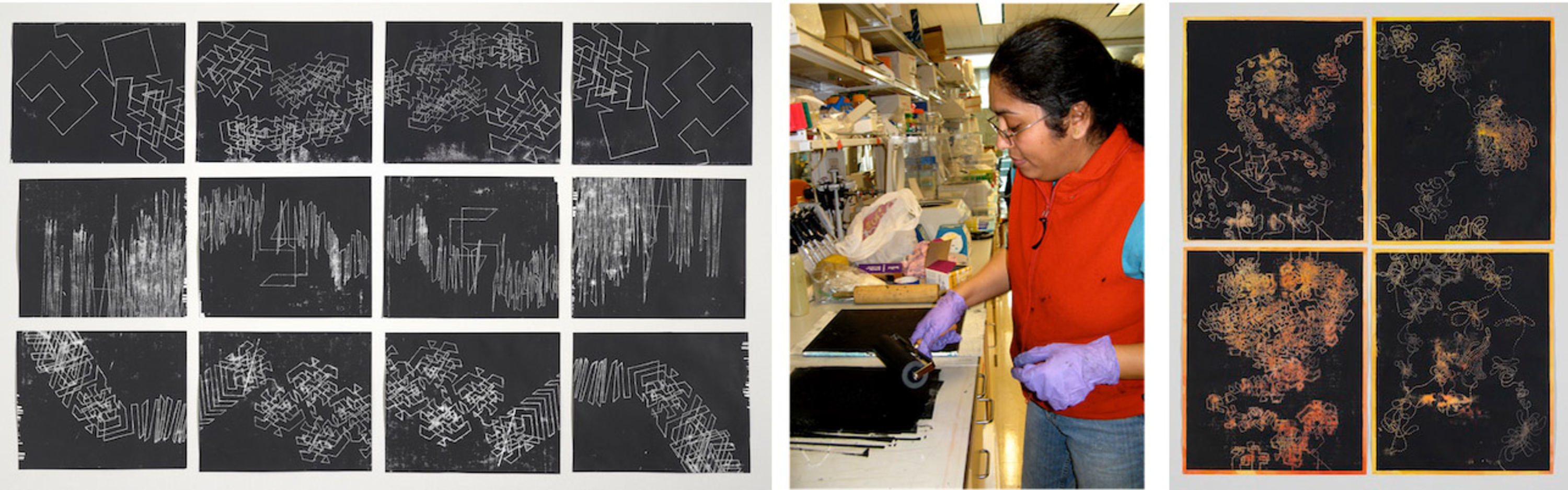
For almost a year, Erez and I made no break-through with the collaborative process. We were worried that I was creating drawings, prints, and artworks that illustrate but do not advance the project. Erez especially wondered why I kept wrestling with the electrical wires as I tried to assemble and create a physical model of the Peano and Hilbert curves. I felt that there was something important about the process of repeatedly folding and unfolding the electrical wires that I was missing.
Summer 2010, I had my Aha! moment by myself while on a trip to the Ekambareswarar (Shiva) Temple in Kanchipuram, India, built in 600 CE. I was struck by two elements of the temple: the hundreds of pillars which appear identical at a distance but which reveal detailed variation up close, and the Shiva linga sculptures which are glimpsed between the pillars (Fig. 5). Like the pillars, each Peano curve is unique, but the distinctive variations are subtle and not immediately apparent. As for the sculptures, the Shiva linga is an abstract representation of God, the form of the formless. However, there also exist sculptures of the Shiva in human form performing the cosmic dance, and it is understood that both types of Shiva sculptures approach the same truth. Perhaps the mathematical models of the genome, floating in a software program, are like the Shiva linga, but there is another reality in which the genomic curve is a corporeal thing in motion, stretching and compressing. The whole line is intelligent; it has memory, and it can fold and unfold itself. Sculptures of the dancing Shiva each capture a different point in time in a dance and, even more, the sculptures are different proportions and sizes. Could I capture moments of the genome’s dance as the dancing Shiva sculptures do, pursuing the dynamic and physical form of something abstract?
I focused on the continuous movement of the genomic line as it folds and unfolds at the microscopic level. I could see that there can be infinite possibilities to folding the electrical wire, or the genomic section, while still complying with the requirements of the idealized, tangle-free Peano curve. Portraying the dynamic movement of a section of the genomic line as a sequence of poses or still images might communicate this complexity. Back in my studio, I quickly manipulated the wire held in my left hand, drawing on Post-Its the resulting silhouettes and forms in seven segments. Each fit uniquely into the two-dimensional square space, just as the genome, regardless of its number of segments, fits into the same miniscule space. The resulting 120 Post-Its is like a collection of animation movie stills; it takes some visual cues from The Simpsons, which I thought would resonate with American viewers (Fig. 6 and Fig. 7).
I began to wonder what we would see if we used a long armature wire, or multiple armature wires, with multiple 7-length segments, to create a physical genome model that could be compressed and stretched. I made a large sculptural model from eighteen coils of 20-foot armature wire, focusing on a dynamic structure with many possibilities, to see how it would inform the project. Over the next few months, I created paintings based on the 120 Post-Its (Fig. 8) and these wire structures, and folded the coils to create a suspended sculpture for Erez and the other researchers to interact with and explore (Fig. 9).

The physical in conversation with the abstract
Gupi: 120 Post-Its opened up an entire world of possibilities for seeing, visual thinking, reasoning, linking, and understanding how the genome folds and unfolds—processes that Erez, the Aiden Lab, other researchers, and I had not considered before. I started seeing my work through new eyes, asking new questions and exploring possibilities beyond What is this? and Where is this going? to What if? and Maybe... As we both shifted the grids and perspectives that come with our separate disciplines, I created a series of mixed-media drawings, Sampling - Beyond Observation: Filling the Gaps (Fig. 10), to suggest some of the many possibilities for the invisible dynamic structure as the genome folds and unfolds in each cell of our body throughout our lives. Erez borrowed the digital images of these mixed-media drawings to continue his work on the problem of genome folding with the Aiden Lab.
Erez: Gupi's massive, extraordinary wire sculptures, and more so the experience of watching her explore the problem of genome folding using the medium of electrical wire, was eye-opening for me. In these explorations, the world of invisible theories crashes into the world of our sensory experience. It made it possible to develop and deploy new sorts of sensory intuition, both visual and tactile, to a problem where our intuitions had typically come up short.
These physical explorations with Gupi’s artwork went hand-in-hand with our mathematical and physical explorations of our genome folding theories. A curve that might be first traced out in 3D space could, for example, be translated into an idealized mathematical trajectory, and from there, it might be examined using a new tool set. Conversely, a mathematical effort to examine the consequences of knotting in the genome could directly benefit from realizing the mathematical knot as a physical object which one could push, pull, stretch, and deform (Fig. 10).
The creative process and Gupi’s serial visual experimentations led me and my team to explore mathematical variants on the curves we use to help model the genome, variants that we may not have otherwise emphasized. For instance, Figure 11A is a traditional representation of the Peano curve. Now, a careful observer will note that the curve is made of line segments with a fixed size. This sort of construction is mathematically natural, and easy to implement on a computer, but it is hard to do with electrical wire! Real materials—like electrical wire, but also like DNA—resist this sort of perfect homogeneity. Our work immediately raised the question: could we construct curves that reflect the heterogeneity of real objects, while retaining the dimension-defying mathematical equivalence to Peano’s curve? And could not such a curve be a superior model of the folded genome as compared to what we had used before? Figure 11B is (part of!) a mathematical response in the affirmative.

Art as manifestation of the possible
Erez: There is much about the folding of genomes that remains mysterious, about which we can only speculate. For instance, several years ago, our lab encountered what we called “superloops” in the genome which arise when stretches of DNA that are extraordinarily far apart along the contour of the chromosome encounter one another in 3D space (Darrow & Huntley et al., 2016). This is a phenomenon which we did not predict, which was hard to explain given our best theories, and whose underlying mechanism remains unknown even today. I suspect that Gupi's mixed-media drawings (Fig. 10) have long engaged with this interface, and we use them routinely as a way of visually evoking this unsettled state of affairs at the frontiers of our discipline (Darrow & Huntley et al., 2016; Rao et al, 2017; Rao & Huntley et al., 2014; Sanborn & Rao et al., 2015b). Here, the discrete, geometrical definiteness of the wire recedes somewhat, making space for something more indefinite: what happens when our simplistic models encounter the vast, unimaginable reality that lies just beyond our theory's grasp.
One of the most suggestive elements of the mixed media drawings is the way in which they provide a representation that integrates diverse modes of thought. In each image, one can observe coherent structures bubble up, as if from a structural welter—here, an idealized mathematical curve; there, the same curve but stretched, compressed, bent, warped—the ideal object as it manifests with real materials. Unlike a scientific diagram, the images are not didactic; they present possibilities without enforcing a single, rigid interpretation. In this respect they are more true to our understanding than any diagram that is presently possible.
Gupi: Focusing on the idea and concept of "unfolding" in my artworks enabled us to reframe our questions. I finally understood that what we had been doing was slowly and continuously shifting from the abstract ideal world of the Hilbert and Peano curves - to the representational ideal world of our initial electrical wire models, drawings, and prints - to the representational real world of the electric wires - to the abstract representations of the real world with 120 Post-Its - to the representational real world of the eighteen coils sculptural installation - and, finally, to the imagined and suggested world of the combined abstract and real mixed-media drawings. Our collaborative creative process had enabled me to “see” that we are following the invisible; the suggested worlds made visible in my art are in a back-and-forth conversation with the advances in Erez’s lab, revealing directions for our shared journey we hadn’t envisioned (Fig. 12).
Supplemental material
Bibliography and further reading
- Aiden, E. L. (2011). Zoom! Science 334 (6060), 1222-1223. DOI: 10.1126/science.1216288
- Aiden, E. L. (2015, October 25). Artwork inspired by the problem of genome folding [Blog post]. News, Aiden Lab. https://news.tc4ga.com/post/132951882413/artwork-inspired-by-the-problem-of-genome-folding
- Aiden, E. L. (2019, March). Untangling the genome: New discoveries on ancient loops in DNA offer clues into gene regulation. Scientific American. Retrieved October 20, 2021, from https://www.scientificamerican.com/article/untangling-the-formation-of-dna-loops/
- Beltz, J. (2011). The dancing Shiva: South Indian processional bronze, museum artwork, and universal icon. Journal of Religion in Europe, 4 (1), 204–222. doi: https://doi.org/10.1163/187489210X553566
- Broad Institute. (n.d.) This Is Broad. https://www.broadinstitute.org/about-us
- Broad Institute. [Ranganathan, G. & Erik-Siren, L.] Unfolding (2012, July 11). [Video]. YouTube. https://www.youtube.com/watch?v=Aj_trjZ7jKE
- Broad Institute. (2015, December 18). Broad Institute Artist-in-Residence - Gupi Ranganathan [Video]. YouTube. https://www.youtube.com/watch?v=5CjYo3h7akc
- Broad Institute. (2020, January 27). Gallery talk: Celebrating art and science at the Broad [Video]. YouTube. https://www.youtube.com/watch?v=5kydyHo79s0&t=2978s
- Christenson, F. (2019, April 23). Mudras: The gestural language of Indian theater and dance. Global Theater, Colgate University. https:// cducomb.colgate.domains/globaltheater/asia/mudras-the-gestural-language-of-indian-theater-and-dance/
- Clegg, E. (2011, December 14). “Unfolding” exhibit blends art and science at the Broad. Broad Communications. Retrieved April 19, 2021, from https://www.guhapriyaranganathan.com/broad_show_opening_dec152011.pdf
- Clegg, E. (2012, April 4). Broad Artist in Residence at MassArt. Broad Institute. https://www.broadinstitute.org/blog/broad-artist-residence-massart
- Darrow, E. M. & Huntley M. et al. (2016). Darrow, Huntley et al. 2016 Media Kit. Aiden Lab - The Center for Genome Architecture - Baylor College of Medicine. http://aidenlab.org/darrowhuntleymediakit2016/
- Darrow, E. M. et al. (2016, August 2), Deletion of DXZ4 on the human inactive X chromosome alters higher-order genome architecture. Proceedings of the National Academy of Sciences of the United States of America 113 (31), E4504-E4512. DOI: 10.1073/pnas.1609643113
- Ferguson, J. (2020, April). Residency: Real science/real art: Broad Institute of MIT and Harvard. SciArt Magazine.Retrieved April 22, 2021, from https://www.sciartmagazine.com/residency-broad-institute-of-mit-and-harvard.html
- Gauguin, P. (1897). Where do we come from? What are we? Where are we going? [Painting]. Paul Gauguin. Retrieved April 24, 2021, from https://www.gauguin.org/where-do-we-come-from-what-are-we.jsp
- Grosberg A. Yu., Nechaev S. K., & Shakhnovich E. I. (1988). The role of topological constraints in the kinetics of collapse of macromolecules. Journal de Physique, 49 (12), 2095-2100. ff10.1051/jphys:0198800490120209500ff. jpa-00210891f, Retrieved October 6, 2021, from https://hal.archives-ouvertes.fr/jpa-00210891/document
- Haughney, K. (2016, July 18). Scientists delve into 'black box' of DNA research. ScienceDaily, Retrieved April 19, 2021, from https://www.sciencedaily.com/releases/2016/07/160718161302.htm
- Haven, C. (2011, November 7). At Stanford's Cantor Arts Center, dancers bring Rodin to life. Stanford News, Retrieved April 19, 2021, from https://news.stanford.edu/pr/2011/pr-dancers-rodin-cantor-110711.html
- Hilbert, D. (1891). Ueber die stetige Abbildung einer Linie auf ein Flächenstück. Mathematische Annalen, 459-460. Retrieved October 6, 2021, from
- http://www.digizeitschriften.de/dms/img/?PPN=PPN235181684_0038&DMDID=dmdlog40
- Huseman, A. (2016, July 18). Scientists cut “Gordian Knot” in the Human Genome, Baylor College of Medicine Blog Network, Retrieved June 9, 2019, from https://www.bcm.edu/news/molecular-and-human-genetics/scientists-cut-gordian-knot-genome
- IBM. (2011, November 2). The genographic project confirms humans migrated out of Africa through Arabia. Phys.org. Retrieved 21 April, 2011, from https://phys.org/news/2011-11-genographic-humans-migrated-africa-arabia.html
- Lerman, L. (2011, February 25). The Genome Dances. Science, 331 (6020), 1027. https//:doi:10.1126/science.1203459
- Lieberman, E. (2010). Evolution and the emergence of structure (No. 3414846) [Doctoral dissertation, Harvard University.] ProQuest Dissertations & Theses Global.
- Lieberman-Aiden, E. & Van Berkum, N. L. et al. (2009). Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science 326 (5950), 289-293. DOI: 10.1126/science.1181369
- National Human Genome Research Institute. (2009, November 19). Genes in Motion [Video]. YouTube. https://www.youtube.com/watch?v=125mSsQzpU0
- Peano, G. (1890). Sur une courbe, qui remplit toute une aire plane. Mathematische Annalen 36, 157-160. Retrieved October 6, 2021, from https://www.maths.ed.ac.uk/~v1ranick/papers/peano.pdf
- Ranganathan, G., Aiden, E. L. & Golub T. (2011, December 30). Unfolding show opening at the Broad Institute, Cambridge, MA [Video courtesy of the Broad Institute of MIT and Harvard]. YouTube. Retrieved April 23, 2021, from https://www.youtube.com/watch?v=Sm4FBvU6p9E
- Ranganathan, G. (2021). Unfolding the Genome - Gupi Ranganathan and Erez Lieberman Aiden. https://www.guhapriyaranganathan.com/broad.html
- Rao, S. S. P. et al. (2014, December 18), A 3D map of the human genome at kilobase resolution reveals principles of chromatin looping. Cell 159 (7), 1665–1680. doi: http://dx.doi.org/10.1016/j.cell.2014.11.021
- Rao, S. S. P. et al. (2017). Rao et al. 2017 Media Kit. Aiden Lab - The Center for Genome Architecture - Baylor College of Medicine. Retrieved April 19, 2019 from http://aidenlab.org/raomediakit2017/
- Rao, S. S. P. & Huntley, M. H. et al. (2017, October 15), Cohesin loss eliminates all oops. Cell 171, 305–320. doi: https://doi.org/10.1016/j.cell.2017.09.026
- Rodríguez, A. M. (2016, September 6). Researchers perform 3-D genome surgery on female's silent X chromosome. Baylor College of Medicine. https://blogs.bcm.edu/2016/09/06/researchers-perform-3-d-genome-surgery-on-females-silent-x-chromosome-and-alter-folding-of-inch-long-loops/
- Sanborn, A. L. & Rao, S. S. P. et al. (2015a). Sanborn, Rao et al. 2015 Media Kit. Aiden Lab - The Center for Genome Architecture - Baylor College of Medicine. Retrieved April 19, 2019 from http://aidenlab.org/sanbornraomediakit2015/
- Sanborn, A. L. & Rao, S. S. P. et al. (2015b, November 24). Chromatin extrusion explains key features of loop and domain formation in wild-type and engineered genomes. Proceedings of the National Academy of Sciences of the United States of America 112 (47), E6456-E6465. https://doi-org.proxy.lib.umich.edu/10.1073/pnas.1518552112
- Shankar, B. S. (2004). Dance imagery in South Indian temples: Study of the 108- Karana sculptures (No. 3148746) [Doctoral dissertation, The Ohio State University]. ProQuest Dissertations & Theses Global.
- Vickers, G. (2015, October 20). Visual elements help tell story of first successful genome surgery. Baylor College of Medicine. Retrieved April 19, 2021, from https://blogs.bcm.edu/2015/10/20/visual-elements-help-tell-story-of-first-successful-genome-surgery/
- Weisstein, E. W. Hilbert curve. Math World, A Wolfram Web Resource. Retrieved April 19, 2021, from https://mathworld.wolfram.com/HilbertCurve.html
- Weisstein, E W. Peano curve. Math World, A Wolfram Web Resource. Retrieved April 19, 2021, from https://mathworld.wolfram.com/PeanoCurve.html
- West R., Burke J., Kerfeld C., Mendelowitz E., Holton T., Lewis J. P., Drucker E. & Yan W. (2005). Both and neither: in silico v1.0, Ecce Homology. Leonardo 38 (4), 286-293. https://doi.org/10.1162/0024094054762089.






